Fair warning: this post is pretty wonkish, even relative to my usual style. (Yikes.)
Robert Metcalfe, the godfather of computer networks, famously stated that the value of a network is proportional to the square of the number of users connected. This became known as Metcalfe’s Law:
The classic example is the telephone. When only two people had telephones, the telephone “network” had relatively little value. When 5 billion people have phones, however, the value of the network is exponentially greater. Because any of those 5 billion people can connect with any of the other 5 billion people (in theory). The economic and social value unlocked through that communications network over the past century has been staggering.
These are network effects, generally considered a good thing.
In short, you want more and more people — and potentially things — connected to a network to create (and hopefully capture) more and more value. This phenomenon is a big part of the success of Facebook, LinkedIn, Twitter, etc.
But network growth isn’t necessarily all rainbows and puppy dogs.
There are negative effects that can scale with a network’s growth too. Traffic congestion is one, as you’ve possibly experienced when your teenage daughter starts streaming videos on three different devices simultaneously (!?) while you’re trying to make it through a Zoom meeting with your boss without the dreaded “Your internet connection is unstable” admonishment. (Ahem.)
We must also sadly acknowledge that the “value” created by users interacting across a network is not an inherently positive function. Boosting the distribution of hate and misinformation through network effects has a decidedly negative impact on society.
But for now, let’s focus on a different challenge of network growth: complexity.
I mean complexity in the scientific sense of a bunch of components interacting in a system, resulting in emergent behaviors and outcomes for the system as a whole. In this case, the network is the system, and the components are everything connected to it (e.g., people, apps, devices, etc.).
Now, complexity isn’t inherently bad. A complex system can be highly innovative and resilient — for instance, in the way that evolution is. But it is not predictable or controllable in the way we typically think of machinery, with fixed inputs, fully-mapped processes, and deterministic outputs. This makes it challenging to manage in the classical sense. And its unpredictability may very well generate undesirable outcomes.
It seems obvious that complexity, too, grows exponentially with the size of the network. The more components you have, the more complex interactions between them:
I call this Metcalfe’s Mirror because it’s a reflection of the same dynamic as Metcalfe’s Law — but a reversed and perhaps distorted reflection of the purely positive outcomes originally predicted. Yes, there’s exponential value to be created and captured through network effects. But there’s also exponential complexity, which can generate significant negative effects beyond the simple linear costs of growing the network.
As with Metcalfe’s Law, it’s hard to quantify these effects precisely. I went with ne, where n is the number of components connected to the network, because it’s a little more than n2 — the mathematical constant e is ~2.71 — and it nods to the complexity of the “natural” world. Also because I’m just a nerd.
Which brings me to martech and companies’ tech stacks. (Thanks for your patience.)
Martech Stacks as “Systems of Systems”
Let’s think of your martech stack collectively as a system or a network. This isn’t too much of a stretch from thinking of it as one big virtual platform. All the people using your stack and all the apps and platforms in it are the “components” contributing to the complexity of this system.
But people and apps/platform don’t contribute equally to that complexity.
Actually, each independent app or platform in your stack can be considered a system unto itself. Assuming you buy into my theory of Metcalfe’s Mirror, the complexity contributed by that app alone is ne for the n users working with it.
Your stack of apps is then actually a “system of systems” (or “network of networks”). In addition to the complexity of interactions within each app, which would be additive, you also have the complexity of interaction effects between apps. Even if two apps don’t directly interact over point-to-point API calls, the effects of one can’t help but mingle with the effects of the other in the larger context of your business.
If you count the number of independent apps/platforms in your stack as p, then your total complexity really increases exponentially by p:
To get a sense of the scale of this growing complexity, plug in a couple of numbers. Say you have a 10-person company with 10 independent apps/platforms in your stack. Your stack complexity would then be (10e)10 = (522)10 — which is 1.52 followed by 27 zeros.
If that same company merely added two more independent apps/platforms to its stack, then the complexity would leap to (10e)12 = (522)12 — which is 4.09 followed by 32 zeros.
That’s a 100,000X increase in complexity!
Admittedly, not every app generates equal complexity. But for the sake of simplifying the math, let’s just assume the complexity averages out across all apps.
And again, complexity isn’t inherently all bad. But it is challenging to manage.
So the obvious conclusion is: use fewer apps. Other things being equal, that’s true. But other things aren’t always equal. There are often significant benefits you gain from the capabilities of different apps added to your stack. That’s why you’re driven to adopt them in the first place.
But you want to weigh the added cost of complexity against the added value they bring.
Platforms Can Significantly Reduce Martech Stack Complexity
There is one other powerful way to simplify a stack: platformization.
You may have noticed that I kept using the qualifier “independent” apps/platforms above. With independent systems, each contributes fully to the exponential increase in complexity. There’s no coordination between them.
Apps that are built on or integrate with platforms, however, benefit from a rationalization of their interaction effects — which reduces complexity. How much that reduces complexity is a function of the coherence of the platform and the degree which a given app/integration takes advantage of it.
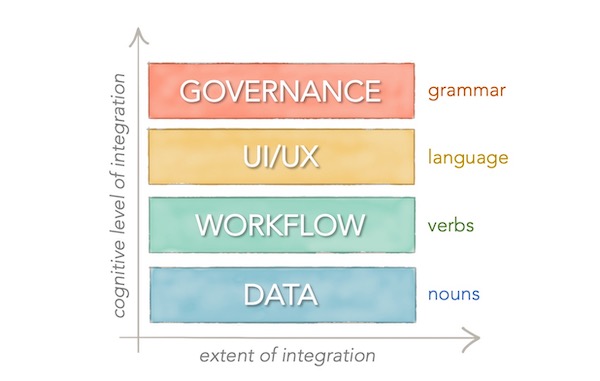
See my post on how not all integrations are created equal: 4 layers of app integrations with SaaS platforms to get a sense of the range of coherence that’s possible across data, workflow, UI/UX, and governance on a platform.
“Platformed apps” a can then be subtracted from the exponent of total apps/platforms p in the formula for your stack complexity:
Of course, platformed apps aren’t completely free of contributing complexity. So the above formula uses a factor of β to estimate the percentage of complexity reduced in the interaction effects of the a apps. β has a value between 0 and 1, with a minimally coherent platform being close to 0 and a very cohesive platform being closer to 1.
For a point on the curve, I’d say Apple’s iPhone platform has β ≈ 0.9.
So to return to our example of the 10-person company with 12 apps/platforms. If 9 of those apps are “platformed,” with a pretty coherent platform that has β = 0.7, then (10e)(12-(0.7)9) = (522)(12-6.3) = (522)5.7 — which is 3.09 followed by only 15 zeros.
That’s 100X quadrillion less complexity that the stack with 12 completely independent apps!
Thanks for powering through this. I know, this has been an especially wonky read, and all this math is pretty handy-wavy (although reasonably derived from Metcalfe’s Law). But I think it does provide a quantitative sense of how complexity grows in martech stacks — and why platforms can bring such tremendous value in reducing that complexity.

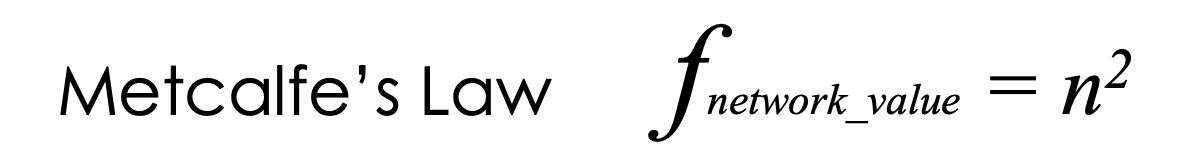

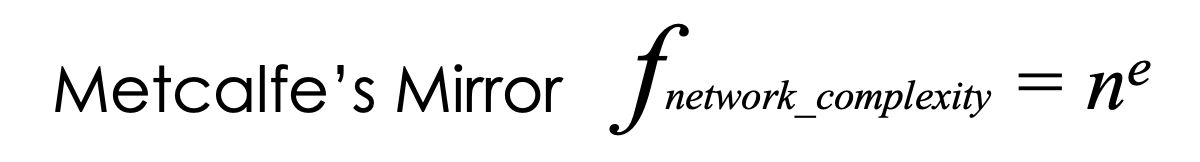
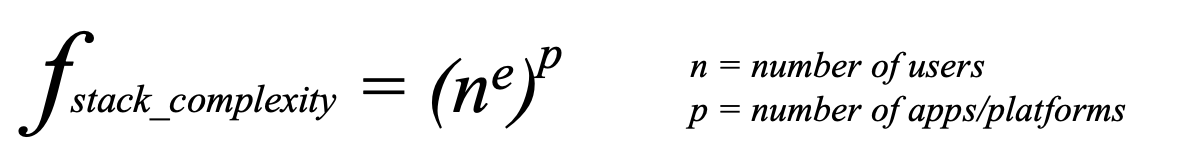
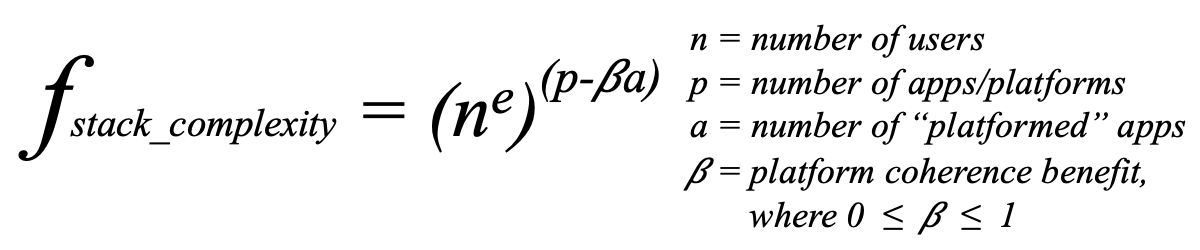
Having grown up in the Telecom’s industry reading this was a full circle moment, I can honestly say I never expected to see Metcalfe’s law applied to MarTech but it makes sense — excellent extrapolation.